Conjunto de algoritmos MENTOR
Etapa 4: Topología de acceso al backbone
Método del acceso Esau-Williams
- Inicializar todos los tradeoffs:
- Seleccionar el tradeoff mínimo:
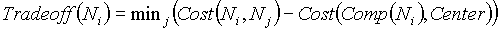
- Si la red viola la siguiente restricción:
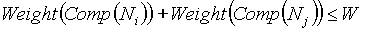
o bien forma trayectoria cerrada entonces:
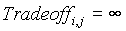
regresar a 2.
- Añadir el enlace que va del nodo "Ni" al nodo "Nj" y fijar
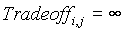
- Si ya están todos los nodos conectados entonces terminar.
- De lo contrario, continuar en paso 2.
Método de acceso basado en Esau-Williams
La heurística asociada con el algoritmo Esau-Williams resuelve problemas relacionados con la creación de un árbol de capacidad mínima (Capacitated Minimum Spanning Tree CMST)
Definición del problema del árbol de capacidad mínima (Capacitated Minimum Spanning Tree CMST):
Dado un nodo central N0 y un conjunto de otros nodos (N1, N2, …, Nn), un conjunto de pesos (w1, w2, …, wn) para cada nodo, la capacidad de enlace "W", y una matriz de costos Cost(i,j), el problema consiste en hallar un conjunto de árboles T1, …Tk, tales que cada nodo Ni pertenezca exactamente a un árbol Tj, y que cada árbol Tj contenga a N0.

La idea central del algoritmo Esau-Williams se basa en la función de tradeoff. La función de tradeoff se diseña para hallar puntos deseables y lograr construir buenos árboles. Inicialmente, cada nodo empieza en un árbol con 1 nodo (él mismo). Debido a que el árbol no estará conectado con el centro, nos referimos al árbol como "componente" en el sentido de la teoría de grafos. Se calcula entonces la función tradeoff para cada nodo:
![]()
El tradeoff asociado con la unión de los componentes Ni y Nj calcula los ahorros potenciales de ir hacia un vecino en lugar de tener una línea hasta el nodo central. El tradeoff es atractivo sólo si éste es negativo. Mientras menor es el tradeoff (o mejor dicho, mientras más negativo) los ahorros serán más atractivos. Sin embargo, la unión entre nodos puede que no produzca un diseño válido. Existe una función que checa que se cumpla la siguiente condición:
![]()
antes de que se permita la unión entre el par de nodos. El algoritmo termina cuando los tradeoff son todos positivos o se ha probado toda la lista de posibles fusiones.
Los pasos del algoritmo Esau-Williams para obtener un árbol
de capacidad mínima (Capacitated Minimum Spanning Tree CMST), son los siguientes:
![]()
Los resultados se pueden resumir de la siguiente forma: Para tráfico homogéneo, el algoritmo Esau-Williams
tiende a producir buenos resultados. Para un número muy grande de nodos, la tasa de falla es mayor.